I think most of us have only been taught Euclidian geometry at school. A ruler and a compass, the solid axioms of the Elements, and here we go!…
But as you probably know, even if it is pretty good to describe quite a lot of things, the Euclidian geometry suffers from some limitations. The famous Greek examples are doubling the cube (or the delian problem), the angle trisection and squaring the circle. We had to wait for the 19th century to show these problems where impossible to solve with the Euclidian geometry (i.e. with a ruler and compass only).
That is why other people invented other types of geometry. Thus, I lately came across some Web articles about origami geometry and I was quite surprised how powerful it is: it is indeed possible to solve some of the impossible problems above with origamis1. It was quite a revolution in my mind ! And where I am the most impressed is that you can achieve a lot with very limited materials: paper and folding…
The thing I did not know is that it exists many publications and theorems about origamis, although this field of research gained most of its popularity in the 20th centry. In this post, I will just give you an example (and a demonstration) of a famous theorem one can find about origami : the Haga theorem.
I like this theorem because it is very easy to understand and shows how you can have interesting geometrical reasonning from origamis. The demonstration is also not very complicated: you do not need more than highschool student geometrical notions to understand it.
The Haga Theorem
The Haga theorem comes from Kazuo Haga, a Japanese retired professor of biology from the University of Tsukuba.
To see what this theorem is, you first need a square piece of paper2. I really encourage you to do it at home because it is very visual.
Fold this square in two. Here is what you get:
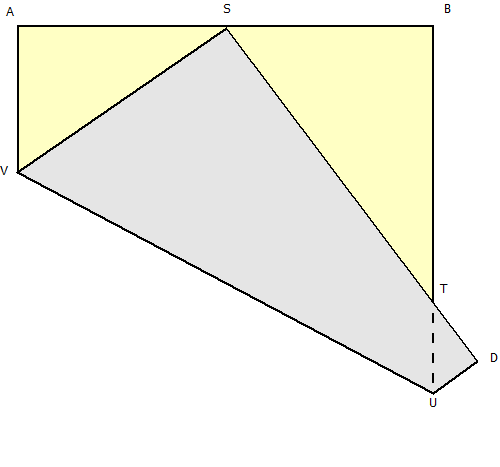
So, the next step is simply to fold the paper so that the corner C goes to the point S, the place where the paper was folded in half. You should end up with something like this::
That’s all! The Haga theorem simply says:
But actually, I prefer to rephrase it like this:
The triangles SAV, SBT and TDU are all Egyptian triangles.
What are Egyptian triangles? Maybe we need some explanations…
Egyptian triangles
You should be familiar with the famous Pythagorean theorem stating that in a right triangle, the square of the length of the hypothenuse (the longest side) is equal to the sum of the squares of the length of the two other sides.
You may also know that the converse of this statement is true: if you have a triangle so that the square of the longest side is equal to the sum of the squares of the other sides, then you have a right triangle.
If the theorem have the name of the famous Greek mathematician of Samos, it seems that more ancient civilizations already know this laws, e.g. the Egyptians.
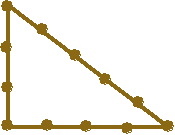
They indeed used a quite powerful tool: a rope with 13 knots evenly distributed. With this rope, they were able to draw right triangle very easily.
Here is how it works:
You take the rope so that you create a triangle with the length 3, 4 and 5. This is a pythagorician triplet, because and that shows that the triangle is a right triangle. You can then used the rope to do draw right angles and build pyramids!
This is where we have our definition: an Egyptian triangle is a right triangle which is similar to this rope-made triangle. Similar means that one triangle has the same shape but maybe with a different scaling. For example, the right triangle with the sides of length 6, 8 and 10 is an Egyptian triangle (because the length are the double of the rope triangle).
Go back to the origami
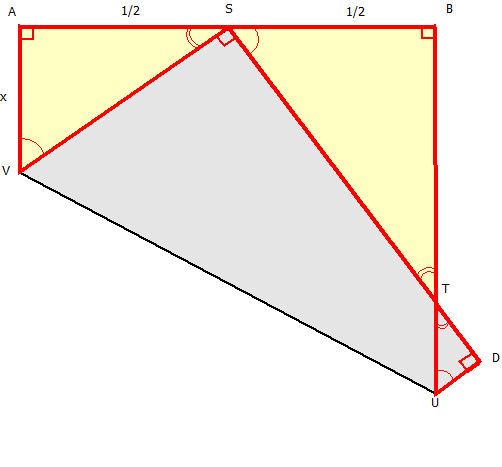
Let’s go back to the Haga theorem, we say we have SAV, SBT and TDU as Egyptian triangles, which means that they are all similar to the (3,4,5) triangle made of rope.
First, we demonstrate that these triangles are similar. We demonstrate this by showing that they all have the same angles. It is a property of similar shapes to have the same angles.
Since the sum of the angles in a triangle is always equal to 180° (or if you prefer). We can show with no difficulties that the angles of the triangles ASV and SBT are the same (as show on the figure).
Concerning angles and they are the same because they are vertically opposite. We can therefore conclude to the similarity between triangles SBT and TDU (and therefore SAV).
Let’s show now that the triangle SAV is Egyptian. For that we will assume the length of the side of the initial square piece of paper is 8. That means the length of AS is 4.
We will now try to find the value of AV.
We have
And Pythagoras says:
Then:
So we have , , and . Hey, that’s an Egyptian triangle!
And since SAV is similar to SBT and TDU, we have show that all these triangles are Egyptian! Q.E.D.
(Origami crane photography author: Andreas Bauer (Origami-Kunst)